The Propulsive Efficiency of the Screw Propeller

The screw propeller efficiency is a major issue that deserves a double explanation: Here is formulated in two different ways (one equation and the other text) this essential concept, of the design of propellers: Of course a good screw propeller efficiency will be different depending on its purpose, thus a propeller helicopters. in hovering flight have zero propulsive efficiency but remain a good screw propeller efficiency. The notion of propulsive efficiency is especially useful in terms of travel costs depending on the distance traveled.

1. The propulsive efficiency equations

2. The propulsive efficiency description

Formulation of the concept of efficiency (1): equations:

The efficiency of a screw propeller efficiency must compare the power supplied to the propeller and the power produced by the propeller. To make significantly the concept of propeller efficiency, the calculation of propeller efficiency must specify how powers are determined: We have seen through the theory of momentum that the propulsive force that we can create with our screw propeller is:

screw propeller thrust:T=m°.(v2-v0)

· with T propulsive force in newtons

· m° Through mass flow in(kg/sec) m° =3,14*density*r²*V2

· v2 the velocity of the fluid downstream of the propeller

· v0 the speed far upstream in m / sec

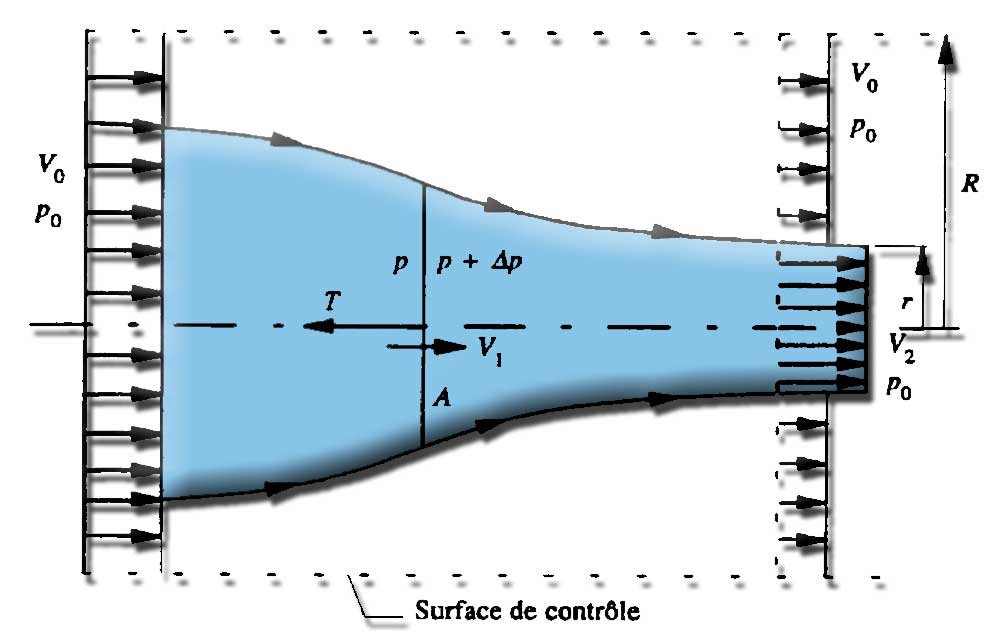
and we found that create thrust is therefore to increase the speed of a fluid mass flow :thrust=m°.(v2-v0)

The power is the product of speed and strength, fluid velocity relation upstream and thrust force gives us "some" idea of the power of our propeller:

· Pu=T.V0

· Pu=m°.(v2-v0).V0

This power is the one that interests transportation because it introduces the concept of useful movement, in fact if the vehicle is to stop, attached to its mooring or brakes locked on the runway, the speed is 0 and therefore our power "useful" Pu is null. Yet our propeller rotates and generates energy so we can not say that its power is zero! So we see the clear need to measure the power of our propeller regardless of the fluid velocity upstream. This is done by calculation of the kinetic power of the fluid upstream and downstream of the propeller.The difference between the kinetic power of the downstream fluid and kinetic power upstream fluid gives us the power of the screw propeller independently of the upstream speed. It's the available power Pa of the screw propeller.

Recall that the kinetic energy is 0.5 X mass X speed² thus :

Pa= (1/2 .m°. V2²) - (1/2 .m°. V0²)

· m° mass flow(kg/sec) m° =3,14*density*r²*V2

· V0 fluid velocity upstream V2 fluid velocity downstream (m/sec)

We note that even if V0 is equal to 0 (vehicle stop) our propeller supplied power. So now we have two notions of power the output power and power available. The ratio of these two powers gives us the propulsive efficiency Rp of our propeller::

· Rp = Pu/Pa

So when our propeller rotates but our car is at stop, Pu is zero and our propulsive efficiency is zero.. So we see that our propulsive efficiency varies with vehicle speed.

The propulsive efficiency gives us this "economic" vision energy, and leads us to transform our equations above it, to highlight the propulsive efficiency Rp

· Pu=m°.(v2-v0).V0

· Pa= (1/2 .m°. V2²) - (1/2 .m°. V0²)

· Rp = Pu/Pa = {m°.(v2-v0)} - {(1/2 .m°. V2²) - (1/2 .m°. V0²)}

· Rp = {2.(V2-V0).V0} / {(V2-V0).(V2+V0)}=(2.V0)/(V2+V0) = 2/(1+(V2/V0))

The propulsive efficiency expressed thus shows that if the difference between V0 and V2 is important propulsive efficiency is low because it wastes energy to move the fluid unnecessarily! Whatever the speed, so we try to have a minimum difference between the vehicle speed V0, and the added speed V2.

The thrust is: T =m°.(v2-v0) we note that if we want to increase the thrust we have the choice between increasing the mass flow m° or increase the difference(v2-v0).

we have seen the best propulsive efficiency Rp advice us of having the difference (v2-v0) as low as possible, so if we want to create an "economic" thrust we have an interest to increase the mass flow! To increase the mass flow, without changing the speed, the only leverage we have left is to increase the diameter of the propeller.

During the construction of the screw propeller so we monitor our efficiency and to the extent possible, we try to have the largest propeller as possible.

Formulation of the concept of efficiency (2) textual description:

the screw propeller Problem datas are:

· The thrust (Newtons) is the product of two factors : Thrust = mass(kg) X acceleration (m/sec²)(see newton:F=m.a). This is the change of momentum that generates the thrust

· the acceleration (m / sec ²) used to calculate the thrust = velocity (m / sec) after the propeller - speed (m / sec) before the propeller

· The mass used to calculate the thrust, is the mass moved in a second, it is the mass flow(kg/sec)

· The power required to produce this thrust is the product of two factors : power(watt)= thrust(newton) X speed(m/sec).

To quantify the performance (quality) of this engine, we must distinguish between two forms of power that are involved in the propulsion:

· The output power observed in terms of displacement, which is useful to us: output power=speed before the propeller X thrust.

· The kinetic power generated by the propeller. This power is calculated according to the variation of kinetic energy of the fluid. (kinetic energy=0.5 X mass X speed²).

o So the kinetic power of the screw propeller =

o = (kinetic energy of the fluid after the propeller) - (Kinetic energy of the fluid before the propeller)

o = 0.5 X mass X (downstream propeller speed)² - 0.5 X mass X (upstream propeller speed)²

o = 0.5 X mass X downstream propeller speed² - upstream propeller speed²

To understand the reality and the usefulness of these two powers, imagine a boat tied up at the dock, or aircraft before launching for takeoff with the brakes applied, which the propeller rotates and produces thrust:

The vehicle is stationary, the velocity is zero, so the output power(useful energy) (output power=upstream speed X thrust) is zero. Yet the thrust of the propeller, and its power is real, the propeller rotates and is powered by an engine that consumes energy! It must therefore be quantified. For this, the variation of kinetic energy applied to the propeller fluid is used. Note that the energy consumed by the propeller when the vehicle is at the stop is wasted! "Good propeller" that earns money by transporting goods with a minimum of energy, it is a propeller that will give the maximum useful energy with minimum kinetic energy !

Efficiency of our propeller is defined as the ratio: output power / kinetic power.

· In other words (by decomposing acceleration to highlight the role of speed):

o Power output = mass flow X (speed_upstream - speed_downstream) X speed_upstream

o kinetic power= 0.5 X mass flow X ( speed_downstream² - speed_upstream²)

· It is essential to note that the power output is proportional to the change in speed and kinetic power is proportional to the square of the speed variation.Thus the speed variation between the input and the output of the propeller increases the kinetic power greater than the power output. We must therefore realize a propeller that produces thrust by changing as little as possible the flow velocity. The thrust is the mass flow X acceleration, it is preferable to increase the mass flow without increasing the speed. A flow is section X speed, so to increase the mass flow without changing the speed the diameter of the propeller must be increased. Conclusion: greater is the propeller , lowest it needs to change the speed to create thrust, and better is its propulsive efficiency!!

One can thus be required to place the propellers as high as possible, so that their diameter is maximum, while allowing the takeoff and landing.